Quadtree and Map Clustering - II

Feb 6, 2019

In the previous post we viewed how to build a QuadTree, now we are going to do the real magic...

Clustering

Clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense, i.e. distance) to each other than to those in other groups (clusters). We’ll need to find all the points which lie in different regions of the map to create groups of points.

struct ClusterPoint {
    let origin: CGPoint
    let points: Int
}

class PGClusteringManager {

    private let quadtree: QuadTree
    private let boxWidth = CGFloat(5.0)
    private let boxHeight = CGFloat(10.0)

    init(quadtree: QuadTree) {
        self.quadtree = quadtree
    }

    public func clusterAnnotationsWithinRectangle(rectangle: CGRect) -> [ClusterPoint] {

        var clusters = [ClusterPoint]()

        let boxArea = calculateBoxAreaSize(size: rectangle.size)
        var xCoordinate = rectangle.origin.x
        var yCoordinate = rectangle.origin.y

        while yCoordinate<rectangle.size.height {
            xCoordinate = rectangle.origin.x
            while xCoordinate<rectangle.size.width {
                let boundingBox = CGRect(x: xCoordinate, y: yCoordinate, width: boxArea.width, height: boxArea.height)
                quadtree.queryRegion(rectangle: boundingBox) { (points) in
                    if points.count != 0 {
                        var totalX = CGFloat(0)
                        var totalY = CGFloat(0)

                        for point in points {
                            totalX += point.x
                            totalY += point.y
                        }
                        let totalPoints = CGFloat(points.count)
                        clusters.append(ClusterPoint(origin: CGPoint(x: totalX/totalPoints,
                                                                     y: totalY/totalPoints),
                                                     points: points.count))
                    }
                }
                xCoordinate += boxArea.width
            }
            yCoordinate += boxArea.height
        }

        return clusters
    }

    private func calculateBoxAreaSize(size: CGSize) -> CGSize {

        let width = size.width/boxWidth
        let height = size.height/boxHeight

        return CGSize(width: width, height: height)

    }

}

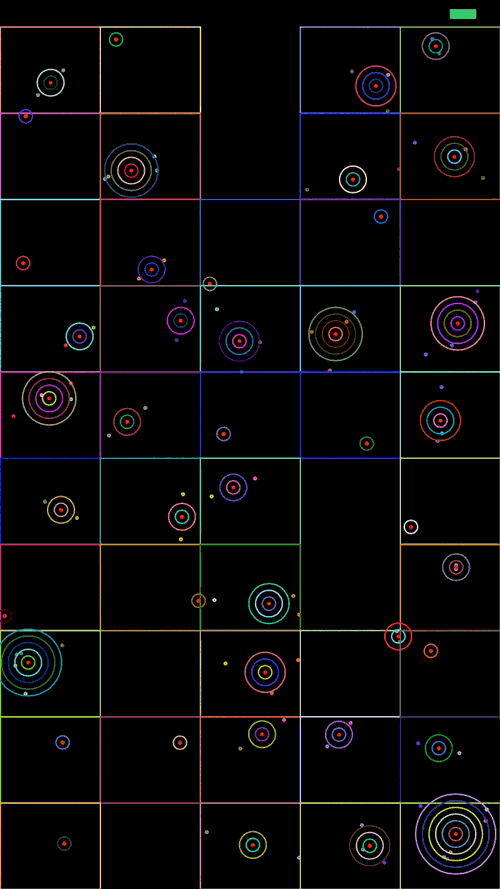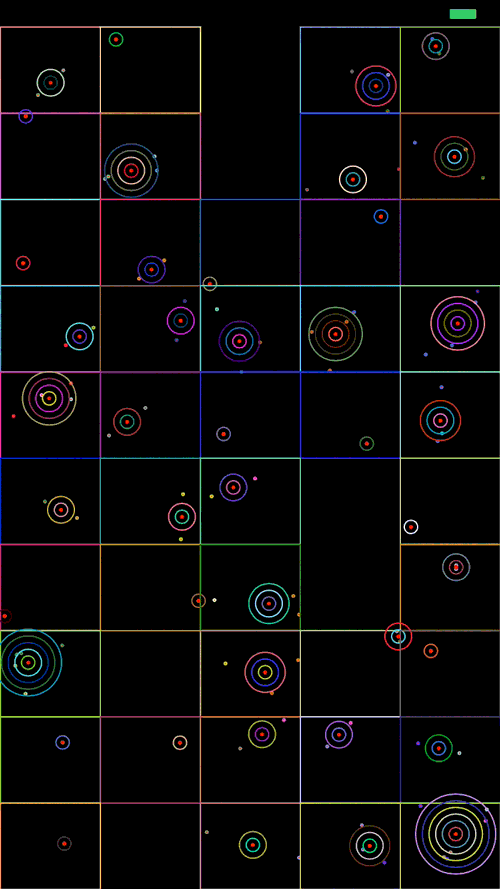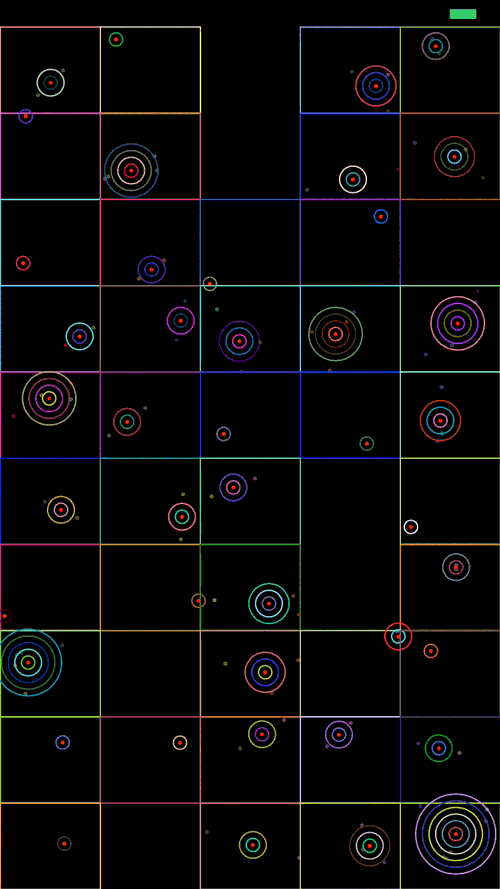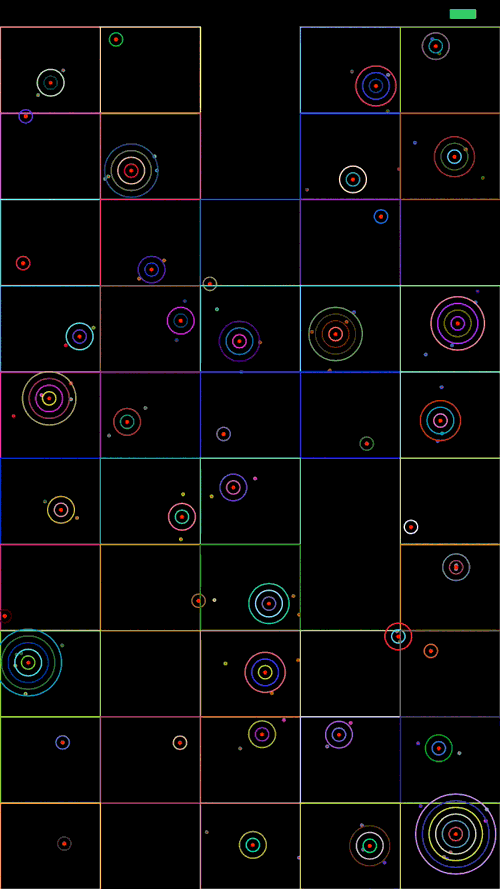
After insert all data in the QuadTree and calling the clusterAnnotationsWithinRectangle function, we'll get something like this:

Awesome!! And now, we are going to check that everything is ok. In the next gift we can see all the points and cluster with their bounding box.